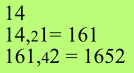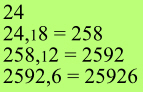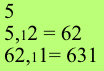Ten-year old Truman Henry Safford was asked:
"multiply in your head 365,365,365,365,365,365
by 365,365,365,365,365,365.
He flew around the room like a top, pulled his
pantaloons over the top of his boots, bit his hand,
rolled his eyes in their sockets, sometimes smiling
and talking, and then seeming to be in an agony,
until, in no more than one minute, said he,
133,491,850,208,566,925,016,658,299,941,583,225!"
Truman Henry Safford was born in America in 1836. He was
a precocious child who
took an interest in all subjects but especially mathematics and astronomy.
He became a professor of astronomy in 1876.
ON THE FLAG
Our mind has the capability to mark a figure, number or thought so that it
stands out. We use this facility very frequently. In mental calculation we
would like to hold the first part of the answer in mind and build it up step
by step, from left to right, until it is complete. The technique introduced
in this chapter for mental multiplication and addition is used in later chapters
and is developed into the general multiplication method in chapter six.
CALCULATING FROM LEFT
TO RIGHT
Since the figures in a number are normally spoken, written and read from
left to right it is easier to calculate from left to right also. And since
the usual methods of multiplication, addition and subtraction work from right
to left it will be necessary for us to learn the alternative strategy of calculating
from left to right. Once this is mastered however we will find that calculating
from the left is easier and more natural. In the Vedic system all arithmetical
operations can be carried out from left to right and this has important consequences
which are briefly described at the end of this chapter and chapter six.
|
The products we get when we multiply 2,3,7 each by 2 (from left to right) are 4,6,14, and here the 6 and the 1 are merged together, to give 474 as the answer. The 3 mental steps carried out, corresponding to multiplying each of
the 3 figures by 2 are: |
The first part of the answer is held in the mind (On the Flag) and is built up digit by digit until the answer is complete.
In summary: if a single figure is to be combined with what is in memory
(as in step 2 above) it is simply tagged on the end; if a double figure is
to be combined (as in step 3 above) the left-hand digit is added to the number
in memory and the right-hand digit is then tagged on the end. It is really
very simple.
|
|
You will find this simple technique easy and efficient, but you will need to practice it. The following exercise will help to establish the method.
After some practice with the sum in front of you you may like to try solving
it after only a brief look at the sum.
![]()
With practice you will find that the sums get easier. You will also find that your memory is strengthened and your mental agility is increased. But do not strain your mind, this will produce an adverse effect; the least force used in solving the sums the better.
This is just the same as multiplying from left to right.
|
We add up in each column. from left to right, and merge the totals
together: |
Addition of numbers is in frequent demand and this method will be found easy and fast once we have formed the habit of calculating from left to right through practice.
![]()
This can of course be extended to the addition of longer numbers or to adding three or more numbers together, but since we are mostly unaccustomed to holding many figures in the head at once we will not take this any further here.
Subtraction from left to right and another addition device will be found
in Chapter 5.
WRITING LEFT TO RIGHT CALCULATIONS
For those interested in calculations done on paper, rather than mentally, the following procedure is probably the best.
|
Starting on the left 8×3 = 24: we put the 2 down as the first
figure |
Alternatively the flagged numbers can be committed to memory rather than written down.
|
|
![]()
It has already been pointed out that calculating from left to right is easier and more natural as we write and pronounce numbers from the left. This makes mental calculations much simpler. It also means that we obtain the most significant figures in a calculation first: if we are multiplying a 6-figure number and we only want the first 3 figures of the answer it is a waste of time and effort to calculate the whole sum, which we would have to do in calculating the usual way from right to left. Other applications of this and an outline of more advanced applications in trigonometry etc. will be found in Chapter 6.
Copyright © 2011 Inspiration Books and its licensors. All rights reserved. 2011
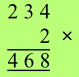
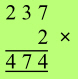
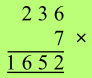 The
mental steps are:
The
mental steps are: