
"Mathematics
is the Queen of the Sciences and Arithmetic the Queen of Mathematics. She often
condescends to render service to astronomy and other natural sciences, but under
all circumstances the first place is her due."
 1
1The three main branches of Mathematics are Arithmetic, Algebra
and Geometry.
Arithmetic deals with number and begins with the number 1 which represents
unity. Unity and wholeness are everywhere.
The system of Vedic Mathematics is based on 16 formulas (or Sutras). For example
By One More Than the One Before (Ekadhikena Purvena in the Sanskrit
language).
Click here to display the list of Sutras.
Starting from number 1 all whole numbers can be generated by using By One More Than the One Before: 2 is one more than 1; 3 is one more than 2 and so on. We will see many other applications of this simple formula as we go on.
1 2 3 4 5 6 7 8 9 10 . . .
Whole numbers are also called natural numbers.
The word digit means the single figure numbers- the numbers 1 to 9 and
0.
Sum means addition.
|
The digit sum of a number
is found by adding the figures in the number.
|
|
a For 17 we get 1 + 7 = 8. b For 401 we get 4 + 0 + 1 = 5. |
![]()
|
The digit sum is found by adding
the digits in a number, and adding again if necessary.
|
|
For 761 we get 7 + 6 + 1 = 14. And as 14 is a 2-figure number we add
the figures in 14 to get So the digit sum of 761 is 5. |
This means that any natural number of any size can be reduced to a single digit: just add all the digits, and if you get a 2-figure number, add again.
![]()
The number nine is very important in the Vedic system. As we will see it has many remarkable properties which make it very interesting and very useful.
The nine digits 1,2,3,4,5,6,7,8,9 used in our number system can be usefully displayed around a circle. As shown below.
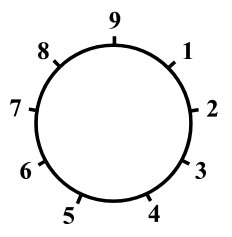
This is known as the 9 point circle. Now suppose we continue numbering round the circle.
It seems reasonable to put 10 after 9, where we have already got number 1. So we can continue numbering around the circle as shown below.
Continue numbering around the circle up to 30 in the boxes provided, numbers 1 to 16 are already shown.
|
Adding 9 to a number does not affect its digit sum:
so 7, 70, 79, 97, 979 all have a digit sum of 7 for example. |
|
We can cast out the nines and just add up the 3 and 4. So the digit sum is 7. Or, using the longer method we add all the digits: 3+9+4+0+9 = 25 = 7 again. |

![]()
Looking again at the 9-point circle, if we count backwards round the circle we see that since 0 comes before 1 it is logical to put zero at the same place as 9. In terms of digit sums 9 and 0 are equivalent and this also explains why we can cast out nines.
|
As digit sums, 9 and 0 are equivalent.
|
This casting out the nines can be used in another way:
|
Any group of figures in a number that add up to
9 can also be "cast out".
|
|
a In 24701 we see 2 and 7 which add up to 9. b In 21635 we can see that 1, 3 and 5 add up to 9 so we cast
these out. |
![]()
![]()
Copyright © 2011 Inspiration Books and its licensors. All rights reserved. 2011